|
Kompozicijska načela:
ritam, kontrast,
ravnoteža, harmonija,
dominacija , jedinstvo
Pitagora
i pitagorejci
Pitagora
i glazba
Harmonijski
niz: građenje muzičkih ljestvica
Proporcije
ljudskog lika kroz umjetnost
Zlatni rez 1
Zlatni rez 2
 Jozef Albers:
Jozef Albers:
Počast kvadratu, 1970.
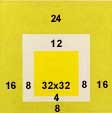 24:12=2
32:16=2 24:12=2
32:16=2
16:8=2 8:4=2
36:16=8:4 (a:b=c:d)
Svi omjeri u slici su izjednačeni. Brojevi 4, 8, 16 i 32 članovi su
geometrijskog niza.
.
 Jozef
Albers: Jozef
Albers:
Počast kvadratu, 1970.
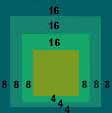 16:16
= 8:8 = 4:4 16:16
= 8:8 = 4:4
I na ovoj su slici omjeri izjednačeni; ali njihov razmak, "korak"
(8,8,8), je jednak. Takav niz je aritmetički niz.
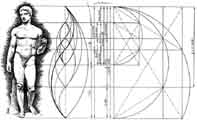
Dorifor (Kopljonoša):
grčki kanon mjera.
Razmjer je u odnosima: a:b=b:c=c:d=d:e=e:f
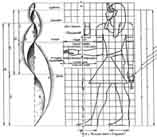
Kanoni proporcija
egipatskih likova
 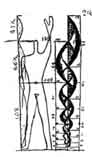
:Leonardo da Vinci
i Le Corbusier:
proporcijske studije u 15. i 20. stoljeću

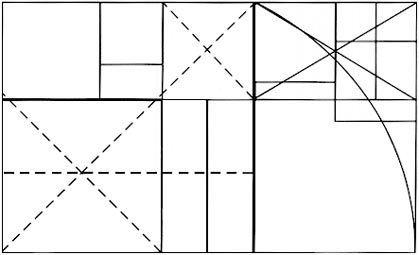
Partenon: odnosi po mjeri čovjeka i prirode
Povlaštena mjesta u formatu
Zainteresirani
za ovakav oblik strukturalne analize (kao na desnim primjerima) mogu
pronaći mnoštvo primjera u knjizi:
Mladen Pejaković: "Zlatni rez"
Nakladnik: Art studio Azinović d.o.o.
Zagreb, Đorđićeva 22
tel./faks: 01/4816-671
|
|
 Omjerom
nazivamo međusobni odnos veličina dvaju elemenata jedan prema drugome.
Jedan lik je dvostruko veći od drugog; jedan je tri puta manji od
drugog; jedan je jednak drugome ali je četiri puta veći od trećeg,
i sl. Omjer tijela prema glavi na "Kopljonoši" jest 1 :
7. Omjerom
nazivamo međusobni odnos veličina dvaju elemenata jedan prema drugome.
Jedan lik je dvostruko veći od drugog; jedan je tri puta manji od
drugog; jedan je jednak drugome ali je četiri puta veći od trećeg,
i sl. Omjer tijela prema glavi na "Kopljonoši" jest 1 :
7.
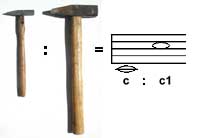
Postavimo u odnose
više elemenata: mali čekić i dvostruko veći; glazbene tonove c1 i
c2 (razmak oktave), dijete visoko 90cm i odraslog čovjeka visokog
180cm te brojeve 13 i 26. Tematski, između njih nećemo naći ništa
zajedničko, ali već na drugi pogled uočavamo kako su svi parovi postavljeni
u odnose 1:2, tj. u omjer dvostruke vrijednosti jednog elementa prema
drugom. Pronašavši na taj način zajednički nazivnik naizgled nespojivim
pojavama počinjemo govoriti o razmjeru (proporciji): postavili
smo u odnos više omjera i više veličina. Kod razmjera je omjer uvijek
sačuvan; razmjer je izjednačavanje omjera. Razmjeri su:
a : b = c : d
a : b = b : c (tzv. neprekinuta proporcija)
a : b = b : (a + b) tzv. "zlatni rez"
Primjerice:
omjer: 4 : 2 (= 2)
razmjerno: 8 : 4 (=2), 32 : 16 (=2), 100 : 50 (=2), itd.
Ujedno uočavamo kako za elemente u omjeru koristimo znak ":"
koji matematički zovemo dijeljenje, pa je tako omjer elemenata uvijek
izračunljiv, izmjerljiv i postavljiv u daljnje odnose, tj. razmjere.
Iz ovog pravila proizlaze progresivni nizovi brojeva, u kojima se
bilo koja dva susjedna broja međusobno jednako odnose kao bilo koja
druga dva susjedna broja. Najpoznatiji proporcionirani nizovi su:
Aritmetički niz: uvijek isti broj zbraja se sa svakim
slijedećim članom niza, što čini sve veličine između dva člana uvijek
jednake, npr:
1, 2, 3,
4, 5... (svaki broj zbraja se sa 1), ili: 1, 4, 7, 10... (zbroj s
3), itd.
Geometrijski niz: uvijek isti broj množi se sa svakim
slijedećim članom niza, što čini da se veličine između dva člana velikom
brzinom povećavaju, npr:
1, 2, 4, 8, 16, 32... (množenje s 2), ili: 1, 3, 9, 27, 81... (množenje
s 3); itd.
Harmonijski niz: počinje od cijelog broja (1), koji se dijeli
na polovinu, trećinu, četvrtinu, petinu, šestinu i tako u beskraj.
Dakle: 1, 1/2, 1/3 (ili 2/3), 1/4 (ili 3/4), 1/5 (ili 4/5), 1/6 (ili
5/6) itd. Pošto je harmonijski niz zapravo aritmetički niz pod razlomkom
(1, 2, 3, 4... - 1, 1/2, 1/3, 1/4...) o njemu se govori i kao o obrnutoj
proporciji. U njemu će mnogi prepoznati tajnu percipiranja
svijeta: Pitagora
uspostavlja glavne konsonante: 1/2=oktava, 2/3=kvinta, 3/4=kvarta;
a Leonardo će zapisati kako ono što je u prirodi u aritmetičkom nizu
(drvored) vidimo kao harmonijski niz (geometrijska perspektiva). Zbog
ovog niza grčki filozof Zenon pobija mogućnost kretanja: ako ispustim
kamen iz ruke, prije negoli padne na zemlju mora prvo doći do polovine
puta; a prije toga do prve trećine; a prije do četvrtine, a prije
do petine... Zapravo, kaže Zenon, ne može uopće ni krenuti!
Fibonaccijev niz: dva člana niza zbrojena međusobno daju slijedećeg
člana niza: 1, 1, 2, 3, 5, 8, 13, 21, 34... Omjeri u ovom nizu su
u "zlatnom rezu": 1, 618... Ovu činjenicu još odavno koriste
umjetnici tražeći u proporcijama (omjerima i razmjerima) odraz načela
stvaranja u prirodi, neki "zajednički nazivnik" koji bi
bio dokaz "traga ruke" zajedničkog Stvaraoca. Najpoznatiji
rezultat tog istraživanja poznajemo pod imenom "Zlatni rez",
razmjer veličina u kojem se manji dio odnosi prema većem kao taj veći
prema cjelini (ukupnom zbroju manjeg i većeg). Formulom:
a : b = b : (a + b)
ili: minor : Major = Major : cjelina
Više o Zlatnom rezu u prirodi i Zlatnom
rezu u umjetnosti. Recimo samo da se otkriće Zlatnog reza pripisuje
starim Grcima, zbog njihovih zabilješki i instrumenata koje su koristili,
ali proporcije Zlatnog reza nalazimo već na Egipatskim građevinama,
što je rezultat njihovih astronomskih i drugih mjerenja prirode kojoj
je Zlatni rez jedno od osnovnih oblikovnih načela. Razmjer Zlatnog
reza izražen je u Fibonaccijevom nizu: 1, 1, 2, 3, 5, 8, 13, 21, 34,
55... Svaki slijedeći broj jednak je zbroju prethodna dva broja.
Traganje za savršenim
proporcijama dovelo je umjetnike stare Grčke do uspostavljanja kanona
odnosno modula, osnovnih mjera, proporcionalnih pravila za prikaz
idealnih mjera ljudskog tijela. Najčešće se koristio odnos veličine
glave prema ostatku tijela, što je kod kipara Polikleta iznosilo 1:6,
a kod kipara Praksitela 1:7; veličina glave išla je 6 ili 7 puta u
veličinu tijela. Prema povjesničaru umjetnosti Winkelmannu Grci su
svoju djecu vježbali u crtanju ljudskih tijela kako bi se naučila
gledati i vidjeti proporcionalne odnose, i tako stekli smisao za lijepo.
Modulima se bavio i Vitruvije u antici, Leonardo da Vinci i Albrecht
Durer u 15.st., te Le Corbussier u 20. st.
Ta ista znanja
o pravilnim odnosima veličina koristi se i za namjerno kršenje pravila,
posebno u karikaturi (ističu se smiješni ili karakteristični elementi
neke osobe) i u tzv. naivnom slikarstvu. Disproporcionalnost je posebno
vidljiva u dječjem crtežu, gdje se semantičkom
(ikonološkom) perspektivom naglašavaju važnije stvari u prikazu;
mnogi umjetnici su stoga uzore tražili upravo u dječjem likovnom izrazu.
Nadalje, proporcionalnost
je važna i u arhitekturi. Još od stare Grčke poznajemo geslo
"čovjek kao mjerilo stvari", što treba prihvatiti na dvije
razine: prvo, arhitektura uvijek ima utilitarno svojstvo, njena funkcija
određuje njen oblik i mjere. To znači da vrata, primjerice, moraju
odgovarati svojom visinom prosječnoj visini osoba koja će ta vrata
koristiti odnosno prolaziti kroz njih. Žlijebovi na stupovima grčkih
hramova (kanelire) imaju širinu ljudskih leđa, kako bi se osobe
koje se okupljaju ispred hrama mogu nasloniti u njih i odmoriti. Drugo,
u projektiranju zgrada koriste se omjeri i razmjeri ljudskih proporcija,
čime se stvara osjećaj sklada i prihvaćanja od strane gledatelja koji
na nesvjesnoj razini u odnosima arhitektonskih elemenata prepoznaje
odnose vlastitog tijela. Stup se, primjerice, omjerom kapitela i stupa
odnosi kao ljudska glava prema tijelu; a razmak među stupovima razmjeran
je rasponu koraka čovjeka.
Posebno je važno
i ovo:
hrvatska riječ "razmjer" na latinskom se zvala "proporcija",
a na grčkom"analogija". Pitagora je, prema pričanju,
prolazeći pored kovačnice čuo cvukove udaranja čekića o nakovanj u
oktavama. Ušavši, vidio je kako su čekići načinjeni u omjeru 1 : 2,
tj. jedan je dvostruko veći od drugog. Time se stvorio analogan, tj.
proporcionalan odnos:
manji čekić prema većemu je kao nota c prema noti c1.
Ta spoznaja omogućila mu je istraživanje sakrivenih odnosa među stvarima
koje je počeo svugdje pronalaziti; stoga je za Univerzum skovao naziv
Kozmos, Uređeni, suprotan od Kaosa. Iz ovih razmišljanja
pojavljuju se riječi struktura (nadređeni red) i korelacija
- sukladnost po istim načelima (dakle, ne po temi, već po sadržaju).
Na ovim principima treba održavati nastavu u školama, to je ono
što pojam korelacije doista znači! Otkrivanjem sakrivenih relacija
učenik ne usvaja samo znanje, već i oduševljenje u promatranju i istraživanju.
Napokon, proporcionalnost
je od izuzetne važnosti pri konstruiranju kompozicija u slikarstvu.
To znači da se već sam format platna ili
papira pažljivo određuje odnosom visine prema širini; najpoznatiji
je tzv. auron, "zlatni pravokutnik", kojemu su stranice
u odnosu Zlatnog reza, ali format može biti i dvostruki kvadrat, ili
u nekom drugom odnosu.
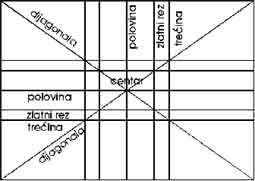
Zatim, svaki format ima u sebi raspoređene nevidljive povlaštene točke
koje utjeću na silnice koje se aktiviraju smještajem likova na ta
mjesta. Najvažniji je svakako centar (polovica formata, vertikalna
i horizontalna) prema kojemu likovi "padaju", "lebde",
"stabilni" su ili "nestabilni". Tu su zatim trećine,
zlatni rezovi i dijagonale, a zatim cijeli mikrosvijet koji nastaje
kombinacijama ovih pravila. Mjesto na kojem se sjeku dva zlatna reza
- vertikalni i horizontalni - nazivamo "optičko središte (ne
brkati sa "očištem" u geometrijskoj perspektivi). Veoma
važan dio likovnog izražaja čini odabir mesta unutar formata na koja
autor smješta pojedine elemente svoje kompozicije. Pogledajmo (samo
slikovni) primjer:

Pietro Vannuci
zvan "Perugino": "Predaja ključeva"



|

 24:12=2
32:16=2
24:12=2
32:16=2
 16:16
= 8:8 = 4:4
16:16
= 8:8 = 4:4










