| Pitagora i glazba | ||||||||||||
|
piše: Petra Zenić |
Glazba je prisutna u svim vremenskim kruženjima (godišnja doba, biološki krug, ritam prirode). Zajedno sa zakonom proporcije ona je zvuk harmonije stvorenog bitka svemira, harmonije koju je već grčki filozof Platon nazvao jedno vidljivo živo biće koje u sebi sadrži sva živa bića istog prirodnog reda. |
|||||||||||
|
|
. | |||||||||||
|
1+2+3+4=10 |
Pred kraj 6. stoljeća prije nove ere došlo je do epohalnih novina u razmišljanju o glazbi. Uveo ih je Pitagora sa Samosa. On nije ostavio glazbenih rasprava, ali podatke o njegovoj glazbenoj djelatnosti saznajemo iz djela njegovih pristaša i učenika. On je postavio matematičke osnove ne samo glazbe već i čitavog svemira. Smatrao je kako u cijelom svemiru vlada red brojeva po kojemu se sve kreće i koji najvjernije izražavaju suštinu stvari i bića, osobito grupa 1, 2, 3, 4 tzv. tetraktis. Brojevi su prema Pitagorinom shvaćanju stalni i nepromjenjivi,a njihov sklad skriva svijet zvukova i harmonije. Utjecaj brojeva Pitagora vidi i u ljudskim osobinama, te otuda potječe mistika i simbolika brojeva (vidi: Pitagorejci). | |||||||||||
|
Oktava:
|
||||||||||||
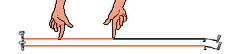 1/2
1/2 Kvinta: 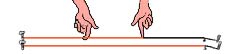 2/3
2/3Kvarta: 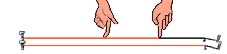 3/4
3/4 |
Tonski sustav kod Pitagore zasnovan je na nizu čistih kvinti. On i njegovi sljedbenici su proučavajući monokord, drevni instrument koji se sastoji od jedne žice razapete iznad rezonantne kutije, otkrili kako su glazbeni intervali proporcionalni dužini žice i ne ovise o njenoj apsolutnoj dužini. Postave li se jedna do druge dvije žice jednake dužine i debljine i jedna od njih podijeli na dva jednaka dijela, ona će biti točno oktavu viša nego duža žica. Nalaze li se dvije jednako zategnute žice u odnosu 3:4 onda je interval tonova između jedne i druge kvarta. Kvinta se dobije ako je odnos žica jednak 2:3. Pitagorejci su zaključili kako suština kvarte, kvinte i oktave nije žica nego broj i jedino su te intervale smatrali konsonantnima, odnosno onima koji zvuče stabilno, prijatno i ostavljaju utisak harmoničnosti, sklada i reda. Sekstu (16: 17) i tercu ( 81: 64) smatrali su disonantnima, odnosno neprijatnima i neočekivanima. | |||||||||||
|
Ova pravila mnogi su primjenjivali i na boje. Najpoznatiji sustav ponudio je Arthur Schopenhauer, njemački filozof iz Gdanjska. On je povezao ovim razlomcima poznate toplo-hladbe parove prema optičkoj ravnoteži. Tako je zelenu i crvenu uravnotežio u količinama pola-pola: 1/2:1/2. Narančastu i plavu je postavio u odnos 1/3:2/3, a žutu i ljubičastu u odnos 1/4:3/4. Na taj način, dva razlomka svakog para uvijek daju jedno cijelo. | |||||||||||
J. Kepler: Harmonija planeta, 1590. |
Primjenjujući
svoja saznanja Pitagorejci su došli do zaključka kako su zvuci u direktnoj
proporciji sa udaljenostima nebeskih tijela. Solarni se sistem prema njihovom
shvaćanju sastoji od 10 planeta koji se kreću u krugovima oko centralne
vatre. Mislili su kako svaki od tih planeta proizvodi svoj ton ovisno
o udaljenosti od mirnog centra u kojem je smještena Zemlja. To je ono
što nazivamo Musica Mundiana ili glazba sfera. Bliže sfere stvaraju dublje
tonove, a dalje i brže sfere stvaraju više. Zvuk koji nastaje na taj način
toliko je rijedak da ga naše obične uši ne čuju. Sveti Augustin je smatrao
kako ljudi tu glazbu čuju kada se nalaze na samrti i da im se tada otkrivaju
najviša znanja kozmosa. Još u 16. st. Johann Kepler je tražio način da prikaže Pitagorin sustav harmonije sfera pomoću pravilnih geometrijskih tijela i tako pronađe rukopis Boga, geometra. Nadao se kako će pomoću njega izračunati putanje planeta; nije mu uspjelo, ali je uz pomoć Tycho Brahea došao do golemih astronomskih otkrića, koje poznajemo kao tri Keplerova zakona. |
|||||||||||
 Ideju
kako će isti razlomci biti ugodni uhu isto toliko koliko i oku zastupali
su i Platon, Plotin, sv. Augustin te mnogi drugi. Najdirektnije ju je
izrekao renesansni arhitekt L. B. Alberti: "Uvjeren sam da je Pitagora
rekao istinu. Priroda se ponaša postojano... Zaključujem da su isti brojevi
čiji zvukovi dobro utječu na naše uši oni koji zadovoljavaju i naše oči
i naše umove.'' Ove proporcionalne odnose moguće je vidjeti ispisane na
tablici koje drži sjedeći lik na poznatoj Rafaelovoj slici "Atenska
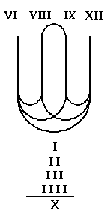
škola". Niz brojeva 6-8-9-12 čine Pitagorinu univerzalnu proporciju;
linije povezuju 6 i 12 u odnos 1/2 (pola-pola), 6-9 i 8-12 u odnos 2/3,
6-8 i 9-12 u odnos 3/4, između 8 i 9 je jedno cijelo. Ispod je ispisan/iscrtan
sveti tetraktis. Ideju
kako će isti razlomci biti ugodni uhu isto toliko koliko i oku zastupali
su i Platon, Plotin, sv. Augustin te mnogi drugi. Najdirektnije ju je
izrekao renesansni arhitekt L. B. Alberti: "Uvjeren sam da je Pitagora
rekao istinu. Priroda se ponaša postojano... Zaključujem da su isti brojevi
čiji zvukovi dobro utječu na naše uši oni koji zadovoljavaju i naše oči
i naše umove.'' Ove proporcionalne odnose moguće je vidjeti ispisane na
tablici koje drži sjedeći lik na poznatoj Rafaelovoj slici "Atenska
škola". Niz brojeva 6-8-9-12 čine Pitagorinu univerzalnu proporciju;
linije povezuju 6 i 12 u odnos 1/2 (pola-pola), 6-9 i 8-12 u odnos 2/3,
6-8 i 9-12 u odnos 3/4, između 8 i 9 je jedno cijelo. Ispod je ispisan/iscrtan
sveti tetraktis. |
||||||||||||
| Literatura: 1. Abraham, Oksfordska istorija muzike 2. Anfilov, Fizika i muzika 3. Muzička enciklopedija 4. Enciklopedijski leksikon - muzička umjetnost 5. Laertje, Životi i mišljenja istaknutih filozofa 6. Dejić, Tajni svet matematike 7. C. Sagan: Kozmos |
||||||||||||

