Pomoć i uputstva za upotrebu
     Harmonijski niz: građenje muzičkih ljestvica
   

piše: M. Huzjak

 

   
    .U srednjevjekovnom školstvu govorilo se o sedam tzv. "slobodnih umijeća ili vještina" - Artes liberales. Osoba koja ih je izučavala i prakticirala smatrala se slobodnom osobom, neopterećenom egzistencijalnim okvirima koje je uslovljavala obrada zemlje (koja je prostorno ograničavala radijus kretanja svom obrađivaču) ili bilo koje drugo zanimanje u kojem praktikant nije razvijao svoju volju, tj. slobodu. Te su artes bile razvrstane u dvije skupine ili stupnja: tri niže ili trivium, te četiri više ili quadrivium. Trivium su činile: gramatika, retorika, i dijalektika (ili logika), a quadrivium: aritmetika, geometrija, astronomija i muzika. Možemo reći kako prvu grupu čine jezične vještine, a drugu matematičke.
     Ovdje bi nam za oko trebala zapeti poslijednja od njih; muzika. Ona je posve ravnopravno svrstana uz bok matematičkim umijećima, negirajući ono što će danas većina smatrati za njenu glavnu karakteristiku - umjetnost. U tom popisu, naime, nema ni traga slikarstvu, kiparstvu ili možda arhitekturi.
   
 

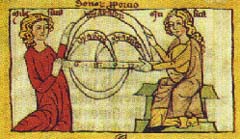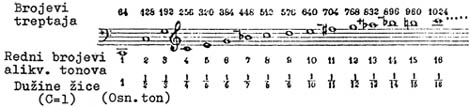
   Našeg iznenađenja neće biti ako smo se prethodno upoznali s Pitagorom kroz tekst o njegovom odnosu prema muzici. Ali pogledajmo prvo jednu srednjovjekovnu sličicu koja ilustrira artes o kojoj govorimo. Na njoj vidimo dva lika kako drže jednu geometrijsku konstrukciju koju očitavamo kako jedno cijelo (gornji luk), jednu polovinu (donji luk), te dvije trećine i tri četvrtine, dakle: oktava, kvarta i kvinta. Tu su prikazani glavni, prirodni konsonanti.

Pogledajmo sada ovaj niz nota i brojeva (koji su frekvencije titranja tih tonova):
   
 

   Radi se o tzv. alikvotnom nizu. Svaki pojedini ton koji nekako izvedemo (odpjevamo, odsviramo...) nosi u sebi, uz svoju temeljnu, još i cijelo mnoštvo frekvencija (broj titraja u sekundi), a to znači i mnoštvo drugih tonova koji se slabije čuju. Ako zatitramo neku žicu, neće titrati samo njena dužina, već i njena polovina, trećina, četvrtina itd nekom drugom brzinom. Osim toga, zatitrati će i okolni zrak, pa materijal instrumenta, pa predmeti u okolici... tako će kod gitare titrati njeno drveno tijelo, ali i zrak u njemu koji čujemo kroz otvor tzv. rezonantne kutije. To sve pojačava zvuk instrumentu, ali mu daje i ono što zovemo boja zvuka. Tako razlikujemo muški od ženskog glasa, violinu od gitare itd. iako se čuje ton iste visine, glasnoće i trajanja. Razlika je, dakle, u broju alikvotnih tonova.
   Uočimo sada koji niz brojeva gradi alikvotne tonove: prva frekvencija iznosi 64 titraja u sekundi (prve tri note su napisane pod bas ključem zbog dubine); drugi je 128 (1:2); treći je 192 (192:3=64, dakle: 1:3); četvrti je 256 (1:4, jer je 256:4=64), itd. Podsjećam: najviše se čuje bazična frekvencija (kažemo da je to ton C), a svaka slijedeća čuje se sve slabije. Taj niz kojim se usitnjuju brzine titraja prpoznajemo kao tzv. harmonijski niz, koji je obrnuto proporcionalan aritmetičkom nizu: aritmetički 1, 2, 3...; harmonijski 1, 1/2, 1/3... Ponovno smo kod Pitagorinih razmjera.

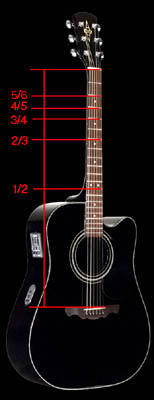
   Pokušajmo sada takvim načinom izmjeriti vrat jedne gitare. Ustanoviti ćemo kako se doista na polovini žice nalazi oktava, na trećini kvinta, na četvrtini kvarta, na petini velika terca, na šestini mala. Tu ćemo najčešće na gitarama pronači i točke koje označavaju tzv. flažolet (samo dodirnuta žica koja dugo odzvanja). Ipak, nakon omjera 5:6 usitnjavanja se više ne poklapaju s prečkama na gitari, a time ni s muzičkom ljestvicom. Tu se kriju problemi mnogih pokušaja stvaranja ljestvice; i zato su prve ljestvice bile pentatonske. Proći će mnoga stoljeća do otkrića osmotonske, a još kasnije kromatske, dvanaesttonske ljestvice. Ipak, sve su u svojoj osnovi imale alikvotni niz, a time i harmonijsku proporciju.
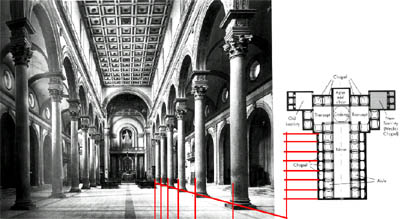
   Uočimo još i kako su prečke na gitari pri vrhu raširene, a zgušnjavaju se prema dnu vrata; obrnuto od zvučne podjele.
 
 
     
       I još jedna muzička opaska: Leonardo da Vinci je zapisao kako slikar mora postupati poput muzičara: tamo gdje je u prirodi aritmetički niz, slikar mora naslikati harmonijski. Provjerimo to na donjoj fotografiji: u prirodi - tj. na tlocrtu - stupovu su međusobno jednako razmaknuti, dakle niz je aritmetički (pomak je uvijek za istu vrijednost). Na fotografiji, međutim, vidimo prividna skraćenja i zgusnuća razmaka između stupova: bliži stupovi imaju veći razmak, udaljavanjem se razmak prividno smanjuje.
   
     
1/2 1/2
1/2
1/3 2/3
2/3
1/4 3/4
3/4

J. Kepler:
Harmonija planeta,
1590.		      Slušajući Leonarda kako pokušava slikarstvu dati isti dignitet koji je muzika oduvijek imala (kao znanstvena disciplina vezana uz matematiku koja oslobađa svog djelatnika, artes liberales) sjetimo se na kraju i Schopenhaureovih odnosa boja, kao i Pitagorine (a kasnije i Keplerove) muzičke harmonije sfera. Sve je ukazivalo (a slutnje stoje još i danas) na jedinstvo ustroja svemira proporcionalnog karaktera (muzičko jedinstvo - jer muzika dolazi od muza, a ne glazbeno jedinstvo jer glazba dolazi od glasa; muzičar je slobodan, on komponira; glazbenik nije), ali i na posebnost našeg doživljaja istog. Naš doživljaj okolice ne odgovara pravom stanju stvari. Simbol ovakve pojave biti će klavir: gledajući u njegovu fasadu vidimo tipke jednake veličine, jednako razmaknute; ali već sam oblik krivulje poklopca podsjeća kako su unutra žice koje daju zvuk u dužinskim omjerima sasvim drugog karaktera, nimalo jednoličnog. Pojaviti će se tzv. Weber-Fechnerov zakon koji kaže da je intenzitet osjeta proporcionalan logaritmu intenziteta podražaja. Drugim riječima, jedno je pred nama, a drugo vidimo (ili čujemo).
Ali to je već druga priča!