|
Zlatni rez: geometrija prirode ili prirodna geometrija |
||
| PRVA
STRANICA NASTAVNE JEDINICE CRTAČKE JEDINICE SLIKARSKE JEDINICE GRAFIČKE JEDINICE KIPARSKE JEDINICE DIZAJN LITERATURA DIDAKTIČKI MATERIJAL LIKOVNI ELEMENTI KOMPOZICIJSKI ELEMENTI LIKOVNE TEHNIKE PJESME PRIČE METODIKA |
Gledajući raznovrsnu pojavnost svoje okolice čovjek o njoj stječe neke intuitivne dojmove. Oblici kod gledaoca dobivaju za njega subjektivne karakteristike – vidi ih kao “vitke”, “zdepaste”, “elegantne” ili ne, sviđaju mu se ili ne sviđaju. Ukus je bitan čimbenik čovječjih reakcija na podražaje: on će birati i oblikovati predmete i okolicu po nekom svom nahođenju, iako najčešće neće moći objasniti što je to što prepoznaje kao lijepo. “Ne znam što je umjetnost, ali znam što mi se sviđa”, izjava je koju često možemo čuti. “Sviđanje” se umeće i u prirodne pojave i oblike, lijepi su zalasci sunca, šarene krošnje stabala u jesen, puževi i školjke sa svojim vijugama; i cvijeće nas privlači sve do uključivanja u manire ponašanja – darujemo ga i njime ukrašavamo okolinu; u gradovima želimo što više parkova i zelenila, držimo kućne ljubimce, vikendom odlazimo u prirodu – prema kojoj očigledno osjećamo jaku pripadnost i ne želimo je se odreći. Ima li u svim tim nevidljivim osjećajima i ukusima nešto izmjerljivo, izračunljivo, čime bismo dokazali i učinili vidljivom tu vezu čovjeka i prirode?
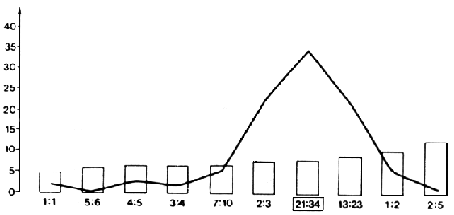
slika 1: grafikon odabira najljepšeg pravokutnika F. Th. Fecher (1876) učinio
je pokus, otada više puta ponavljan. Ispitanicima je ponuđeno deset
pravokutnika različitih omjera (odnosa stranica), između kojih je najveći
broj ispitanika izabrao jedan određeni sa omjerom 21:34 kao najljepši
(P. von Naredi-Rainer: Arhitektur und Harmonie, Dumont, Köln, 1982).
(slika 1) Definicija zlatnog reza
govori o razmjeru – što znači o odnosu dvaju omjera. “Manji dio prema
većem odnosi se jednako kao veći dio prema cjelini”. Ili: “minor:major=major:cjelina”.
Ili: “ A:B=B:(A+B)”.
Drugi način konstrukcije je da kvadrat stranica 1:1 prepolovimo po okomici, i spustimo dijagonalu polovice (AB) na bazu. Iz novodobivene završne točke baze (D) podižemo okomicu u C i zatvaramo kvadrat. (slika 3)
Treći način je malo duži: dijagonala kvadrata stranice 1 koja iznosu korijen iz 2 prenese se šestarom na produženu stranicu kvadrata. Omeđuje se pravokutnik kojem su duže stranice korijen iz 2, a kraće 1. Ponavlja se isti postupak, tj. dijagonala pravokutnika korijen iz 2 koja iznosi korijen iz 3 prenosi se na produženu stranicu itd., dok se ne stigne do pravokutnika korijen iz 5. Tada se povuče simetrala na dulje stranice i iz donjih vanjskih kuteva se dižu lukovi kojima je radijus polovica dužine stranice do sjecišta s gornjom stranicom. Iz tih točaka se spuste okomice koje zatvaraju kvadrat. S obje strane kvadrata preostala su dva manja pravokutnika koji svaki ponaosob s kvadratom daju zlatni pravokutnik. (slika 4) Ovim konstrukcijama smo dobili dvije dužine u omjeru koji čini bazu i stranicu onog kvadrata koji su većina ispitanika prepoznali kao “najljepši”. Za njegove stranice smo rekli da su bile u odnosu 21:34. Rezultat tog dijeljenja iznosi 0,617647… iracionalni broj, matematički nemjerljiv. Međutim, u
13. st. jedan je matematičar, Leonardo iz Pise zvan Filius Bonaccio
postavio aditivni niz brojeva u kojem je svaki slijedeći broj jednak
zbroju prethodna dva: 1:1:2:3:5:8:13:21:34:55:89:144… a koji
je po njemu dobio ime Fibonaccijev niz. Primjećujemo naš omjer
21:34 kao dio tog niza, a računanje će pokazati da svi brojevi ovog
niza podijeljeni sa svojim sljedbenikom, prvim većim brojem,(npr.34:55)
uvijek daju rezultat 0,6…, dakle praktički konstantan razmjer kroz cijeli
niz – čime smo zagospodarili neuhvatljivim iracionalnim brojevima sa
beskonačnim razlomkom. Obrnuti postupak, dijeljenje većeg sa prvim manjim
članom niza davati će konstantnu aproksimativnu vrijednost 1,6. Tako
su zapravo svi brojevi Fibonaccijevog niza u grupama po tri člana (npr.
8:13:21) u zlatnom razmjeru. Osnovna mjera zlatnog kvadrata tako iznosi
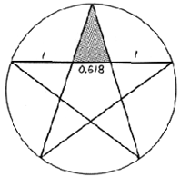
1:1,618. Oznaka za zlatni rez je Kako još možemo doći do zlatnog reza? Recimo, rasijecanjem kružnice na pet jednakih dijelova, što se postiže ovako (slika 5): radius kružnice (BD) dijeli se na pola (E) i povezuje sa okomicom nad centrom (C); dužina EC se spušta na dijametar (AD) u točku P, koja se opet spaja sa točkom C; dužina CP se prenosi na obod kružnice – točka P1. P1C ulazi pet puta u kružnicu, bez ostatka. Ako dobivene vrhove spojimo, dobili smo pravilan pentagram, čiji presjeci dužina krakova ponovno čine pravilne zlatne rezove ( c(3):b(5)= b(5):a(8) , 3:5=5:(3+5=8) ). (slika 6) slika 6: zlatni odnosi krakova unutar pentagrama
slika 6: zlatni odnosi krakova unutar prentagrama U središtu petokrake zvijezde nalazi se manji pentagram čije dijagonale iscrtavaju novi, manji pentagram, postavljen naopako. Njegovi su krakovi opet u omjeru zlatnog reza. U manjoj je zvijezdi još manja, i tako se pentagram beskonačno kopira sam u sebe (slika 7). Pitagorejci su petokraku zvijezdu nazivali pentalfa, jer je sastavljena iz pet slova A, i bila je tajni znak njihovog bratstva.
slika 8: cvijet jabuke i njen presjek
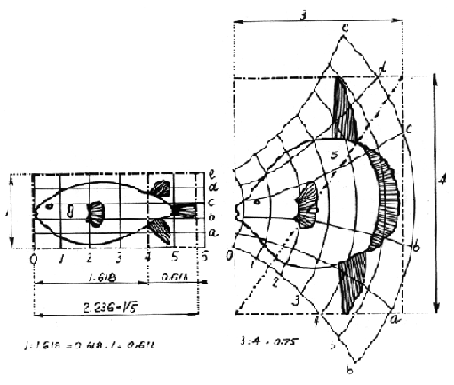
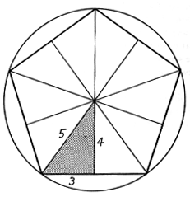
Peterokut još nije iscrpio svoje mogućnosti. Povezivanjem dva susjedna kuta s centrom čini trokut, koji prepolovljen daje tzv. Pitagorin trokut, pravokutan, sa stranicama 3-4-5, odnosno baza 3 : hipotenuza 5 = 0,6. Ili skraćeno baza1: visina1,6 = 0,618 , zlatni odnos (slika 9). I vanjski krakovi zvijezde čine trokute sa jednakim odnosima (slika 10). I takvi trokuti su prepoznatljivi u prirodi – pogledajmo metriku rasta cvjetova na slici 11.
slika 9: Pitagorin trokut u pentagramu slika 10: trokut sa zlatnim omjerima u pentagramu
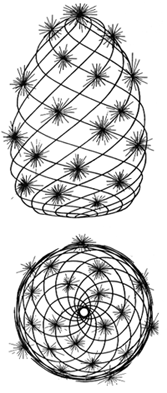
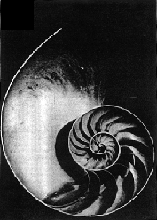
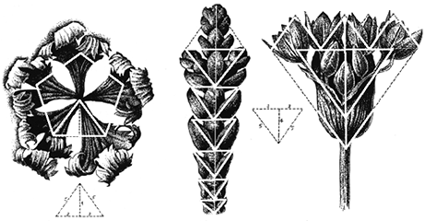
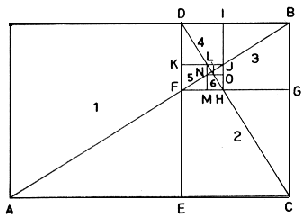
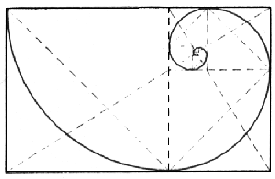
slika 11: metrika rasta cvjetova po Pitagorinom trokutu Načinimo i najkompleksniju konstrukciju. Iz osnovnog kvadrata 1:1 konstruirajmo zlatni (slika 12), i u novom pravokutniku izvucimo dijagonalu AB. Na sjecištu starog brida DE dobivamo točku F iz koje povlačimo paralelu do G. Tako smo desni kvadrat DECB presjekli na dva manja- jedan ponovno jednakostraničan (FECG), i jedan u zlatnom rezu (FGBD). Nova dijagonala (DC) i novo sjecište (H) prelamaju novi zlatni kvadrat na dva manja, opet jednakostraničan i zlatni, ali drugog, vertikalnog, usmjerenja (DFHI). Novim dijagonalama i novim sjecištima stvaraju se rotacije sve manjih zlatnih i jednakostraničnih kvadrata do određenog centra. Ako sada ubodemo šestar u toku D i spojimo gornji lijevi kut s točkom E, zatim ubodemo u točku F i spojimo E sa G, ubodemo u H i spojimo G sa I itd., dobivamo dinamičnu spiralu. Cijelu ovu konstrukciju nazivamo vrtložni pravokutnik, i on čini osnovu rasta mnogih organizama u prirodi. Pogledajmo najočitiji primjer školjke, pa suncokreta, uzoraka paunovog repa ili češera (slika 13).
slika13: školjka, suncokret, paunov rep i češer - neki primjeri dinamične spirale
slika 14: ribe različitog izgleda ali jednake strukture
Miroslav Huzjak
Literatura:
György Doczi - The Power of Limits, Shambala & Boston
i London, 1994. |
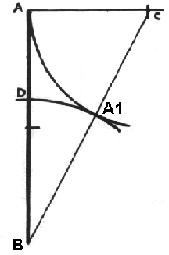 slika
2: konstrukcija z.reza 1
slika
2: konstrukcija z.reza 1 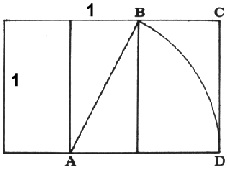 slika 3: konstrukcija
z. reza 2
slika 3: konstrukcija
z. reza 2 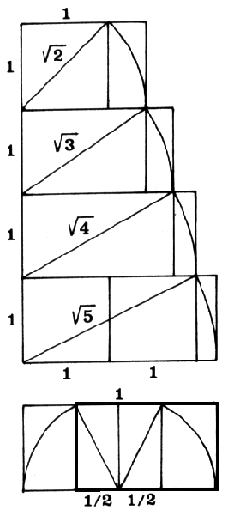 slika
4: konstrukcija z. reza 3
slika
4: konstrukcija z. reza 3 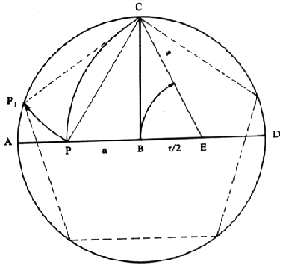 slika 5:
konstrukcija pentagrama
slika 5:
konstrukcija pentagrama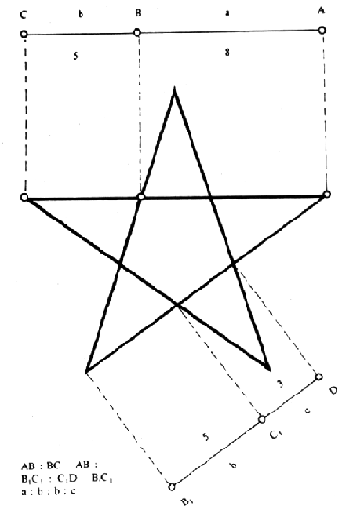
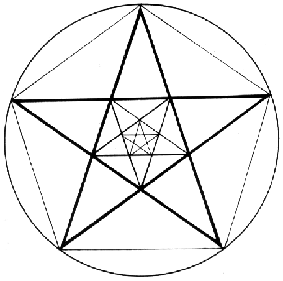 slika 7:
kopiranje pentalfe unutar sebe
slika 7:
kopiranje pentalfe unutar sebe 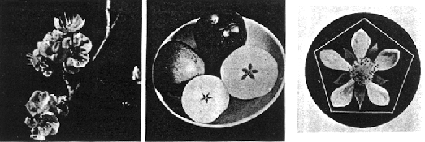
 slika
12: konstrukcija vrtložnog pravokutnika
slika
12: konstrukcija vrtložnog pravokutnika