Nerijetko, govoreći o nečemu što je lijepo i korisno, kaže se da je "prirodno". Neosporna je ljudska opčinjenost prirodom i koliko god se od nje odmicali, nekako se uvijek vraćamo onom iskonskom i onome što zapravo - jesmo. Jer čovjek je tek priroda u malom. Usprkos mnogim tehnološkim dostignućima, on je još uvijek živo biće i kao takav podložan promjenama u prirodi, njezinim pravilima i zakonima. Ritmičnost prirode je neosporna. Svjedoci smo pravilnih izmjena i mjena koje se u njoj dešavaju. Ovaj članak trebao bi tek skrenuti vašu pozornost na taj ritam i koliko smo zapravo o njemu ovisni.

  Krenimo od najupečatljivije ritmičnosti koje smo svakodnevno svjesni - izmjena dana i noći. Ono što je interesantno u tom neprekidnom ponavljanju "iz dana u dan" jest ritmičnost i pravilnost tog ponavljanja. Ono, govoreći iz ljudske perspektive, ne traje uvijek vremenski točno. Ovisno je o godišnjem dobu koje pak opet ritmično dolazi i prolazi ovisno o položaju Zemlje u svojoj putanji oko Sunca. Tako su najdulji dani u vrijeme ljeta - Zemlja je tada najbliža Suncu. Najkraći su kada je najudaljenija - zimi. Na dijelovima zemlje gdje traje "duga noć" koja zna potrajati i do šest mjeseci vrijede neka druga pravila, ali i ona su pod okriljem ritma na koji se priroda tog podneblja navikla. Ovdje dakle impliciramo na važnost tih izmjena za ljude, životinje, biljke, klimu i sav živi i neživi svijet pod nebeskim svodom. Primjerice, sjemenka neke biljke dobro poznaje svoj "unutarnji" ritmični sat koji joj dopušta da klije kada su uvjeti za to najbolji. Stoga će ona čekati dulje dane, ugodnu klimu i sve što ono nosi sa sobom.
  Čovjek bi bez spavanja mogao preživjeti vrlo malo. Ljudi su svoj počinak i rad orijentirali upravo u skladu s izmjenom dana i noći. Takav "ritam života" omogućuje im pravilnu izmjenu potrošnju energije i njezino obnavljanje u snu.

  Već spomenutu izmjenu godišnjih dobi mogli bismo shvatiti kao nužnu promjenu, nanovo ritmičko nizanje ovog četvorca koji omogućuje prirodi da se mijenja, raste i umire te ponovo rađa. Promatrajući godišnja doba mnogi govore o ljetu i zimi kao dva ključna trenutka, a o proljeću i jeseni kao uvertiri za spomenute. Tako je primjerice jesen razdoblje koje nas lagano uvodi u strahote zime. I ljudi i životinje su u tome prepoznali vrijeme za posljednje pripreme.
  Priroda je pritom bila darežljiva i jesen obogatila plodovima koje marljivi ljudi i životinje sakupljaju za kasnije uživanje, tijekom zime koja "ubija" prirodu. Ritmičnost ovih ponavljanja jest ono što drži svijet živim i svaku anomaliju na tom području sav život na zemlji osjeća kao šok.
  Tako smo svjedocima masovne histerije i pojave bolesti uzrokovanih nepravilnošću u klimatskim uvjetima na zemlji. Proljeće kao da više ne postoji, ili se bar njegovo vremensko trajanje jako smanjilo. Zima je protjerana visokim temperaturama koje su zbunile sav živi svijet. Tako smo i ove godine mogli čuti o visibabama u 12 mjesecu koje su promolile iz zemlje misleći da je počelo proljeće. Drveće je propupalo pa opet izgubilo pupove poradi iznenadnog snijega. Neritmičnost je oduvijek za život značila anomaliju.

  Zemljin satelit Mjesec obilazi Zemlju. Njegova putanja traje onoliko koliko po zemaljskom vremenu traje mjesec dana (prepoznajte li analogiju?) Neosporan je Mjesečev utjecaj na plimu i oseku. One se, opet ritmički, izmjenjuju dva puta tijekom 24 sata. O tome koliko utjecaja ima na ljudsku psihu, mnogi su govorili, a malo je dokaza. Ipak, uzmemo li u obzir da je ljudsko tijelo najvećim dijelom sastavljeno od vode, moguće su analogije.

  Valovi koje promatramo na pučini slijede gotovo opipljiv ritam. Kako oni uzrokovani vjetrom, tako i oni nastali bacanjem kamenčića, nose svoju ritmičnost i elegantnost pokreta, slijedeći zakonitosti prirode do trenutka dok ne nestanu. U ovakvim pojavama, kao što je gibanje vode, ali i mnogim drugima, postoje zapažanja koja bismo mogli nazvati kaotičnima. Naime, znanstvenici su primjetili nepravilnosti u ritmičnim događanjima koja najradije nazivaju kaosem. Ipak, kasnijim se promatranjima došlo do zaključka kako se i u kaotičnim zbivanjima nerijetko nalazi red i ritam. "Osobito se to odnosi na neke aspekte nepravilnih gibanja kao što su klimatske promjene, turbulente pojave u tekućinama, varijacije brojnosti biljnih i životinjskih vrsta, srčane aritmije... Takve nepravilne pojave ostvaljale su znanost velikim dijelom zagonetne sve do zadnje četvrtine 20. stoljeća. Tek posljednjih dva desetljeća znanstvenbici su usmjerilki svoju pozornost na zakonitosti takvih nepravilnih pojava" (Kaos, Gleick)

  Ljudi su tako od pravijeka bili svjesni prirode oko sebe, štovali su je i imitirali. Tako u plemenskim i narodnim plesovima nalazimo neospornu vezu oponašanja ritama iz prirode. Bilo kakva odstupanja od onog zadanog, za nas predstavljaju šok i osjećaj nepravilnosti. Laste odlaze na jug u jesen, vraćaju se u proljeće. Drveće gubi svoje lišće u jesen i ponovo se pokriva zelenilom u proljeće. Životinje koje spavaju zimski san bude se na prve znake proljeća. Jesen, proljeće, jesen, proljeće..smrt, život. Mnogi su analogno tome usmjerili svoja razmišljanja o ljudskom vijeku kao beskonačnom - buđenje nakon smrti, novi život.

  Religije svijeta temelje se na shvaćanju kako poslije zime našeg života odnosno naše smrti slijedi novi početak, novo buđenje. I iako najčešće govorimo o novom životu duše koja egzistira na "drugom nivou" od onog u kojem sada obitavamo, okruženi prirodom, mnoga su shvaćanja povezana s njome i govore o reinkarnaciji, ponovnom rođenju upravo ovdje i tu. Reinkarnirali se mi ili ne, neosporna je činjenica da je i smrt važna i da je dio tog "ritma". Mi, živi, možemo tome svjedočiti jer promatrajući mrtve vidimo kako priroda uzima ono što je dala i time hrani daljnji život. O svemu će svjedočiti crni humor koji bi ovo jednostavno preveo kao: zelena salata najbolje raste u vrtovima kraj groblja. Profinjenije bismo to mogli oprimjeriti mrtvom lešinom miša koji djelomično postaje hrana ličinkama, djelomično biljkama. Dakle, živi svijet ne bi opstao bez smrti.
  Naizgled devastirajuća činjenica odumiranja pojedine vrste, ipak, prema nekima, slijedi svoja određena pravila. Tako primjerice u ledenim pojasevima populacije voluharica i lemara rastu i smanjuju se unutar urednog četverogodišnjeg razdoblja.

  Kako smo mi ljudi sebi sami najinteresantniji, priču bismo možda i završili upravo s - čovjekom. Polazeći od DNK, nosioca života, kako neki kažu, i njegove pravilne, nadasve ritmične strukture, pa krenuvši dalje prema radu srca koji je najjednostavniji primjer za ritam, preko disanja gdje izmjena udisaja i izdisaja prati svoje zakonitosti i s tim u skladu nosi svoj ritam, svoju pjesmu - pa sve do same smrti...zaključit ćemo da smo mi sami u središtu ritma prirode. Njezin smo dio i njezina sveukupnost. Nisu nam potrebni primjeri ritmičnih pomicanja kontinenata kada tu naglašenu ritmičnost osjetimo svaki put kada stavimo ruku na grudi. Stoga, nakon svih ovih promišljanja nismo zapravo odgovorili na gotovo ni jedno pitanje. Mogli bismo jedino doći do zaključka da se ritam prirode neosporno zadaje i kao takav treba biti priznat. Jednostavnije rečeno, život bismo mogli zamisliti kao ples prirode i čovjeka gdje svi partneri moraju poštivati zadani ritam ili će si gaziti po nogama.

  Mnogi statističari prilikom svojih proračuna, bilo u korist istraživanja stanja tržišta ili ponašanja Egipatske rijeke Nila, koriste Gaussovu krivulju. Ona predstavlja standardnu, tzv. gausovu tj. normalnu raspodjelu. Govori o prirodi nasumičnosti. Smisao je u tome da kad se stvari mijenjaju, pokušavaju ostati u blizini točke prosjeka i uspijevaju se raštrkati oko prosjeka po glatkoj krivulji. Ali mnogi su primjetili da takav način pronalaženja staza kroz kompleksnost pojava ima svojih nedostataka.

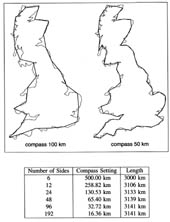
  Možda naizgled nepovezani, promatrani pojmovi poput rijeke Nila i ekonomskog stanja na tržištu, usko su povezani: matematičar Mandelbrot je promatrajući stare zapise o visini Nila ustanovio da je Nil neobično promjenjiv, žestok, plaveći nekoliko godina, a povlačeći se sljedećih. Mandelbrot je ove promjene razvrstao kroz dvije vrste učinaka, poznatih i u ekonomiji, a nazvao ih je učinkom Noe i Josipa.
  Noin učinak predstavlja isprekidanost- kada se količina mijenja, mijenja se gotovo proizvoljno brzo. Ekonomisti su tradicionalno smatrali da se cijene glatko mijenjaju, bilo brzo ili polako, međutim cijene se mogu mijenjati u trenutnim skokovima, jednako brzo kao što se mijenja mišljenje u glavi burzovnih mešetara.
  Josipov učinak znači postojanost - jer poplave i suše uvijek su postojane. "Usprkos skrivenoj nasumičnosti, što dulje jedno mjesto trpi od suše, vjerojatno će trpjeti još i duže". To bismo nazvali trendom prirode koji nastaje i nestaje jednako brzo.

  Takovo razmišljanje koje se temelji na isprekidanosti, ne nalazi mjesta u geometriji gdje su likovi i tijela crte i plohe, krugovi i kugle, trokuti i stošci. Euklidska geometrija koju i dan danas uzimamo kao temeljnu, dakle ipak ne objašnjava u potpunosti svijet.

  "Oblaci nisu kugle, planine nisu stošci, munja ne putuje pravocrtno. Nova geometrija odražava oštar a ne zaobljen svemir, hrapav, a ne gladak. To je geometrija udubljenog, izbodenog i razlomljenog, izvinutog, čvornatog i isprepletenog." Pritom razumijevanje složenosti prirode inzistira na shvaćanju da složenost nije tek slučajna i nasumična. "Bilo je potrebno vjerovanje da zanimljivi dio puta njezine putanje (misli se na munju) nije njezin smjer već raspodjela cikova i cakova".

  U skladu s tim, proučavajući obalnu crtu možemo primjetiti da njezina duljina ovisi o našem pristupu njezina mjerenja: naime, uzmemo li šestilo namješteno na duljinu jednog metra i pomičemo li ga duž obale, dobit ćemo broj koji označava približnu procjenu duljine jer takovo šestilo preskače krivulje i zavoje manje od jednog metra.
  Namještajući šestilo na duljinu manju od metra dobit ćemo nešto veću duljinu jer smo sada uzeli u obzir više pojedinosti. Međutim, smanjimo li opet šestilo, novi broj će opet biti drugačiji. I tako bismo mogli u nedogled. Zanimljivo je da iako se duljina obale tako neprekidno povećava, naš razum nam govori da ćemo na kraju ipak dobiti konačan broj, konačnu vrijednost duljine obale.
  Međutim, što nam je mjerilo manje, to je ta duljina veća i veća, a mi neprekidno otkrivamo sve manje i manje podzaljeve, poluotoke i slično, koji tek čekaju da budu izmjereni. Prava istina je da bi naše mjerenje moglo stati tek na razini atoma, ako i tamo.

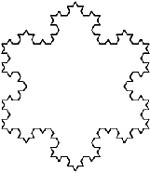
  Dakle, euklidske mjere, duljina, dubina i debljina, ne obuhvaćaju bit nepravilnih oblika od kojih se priroda zapravo i sastoji. Dodajemo stoga i dimenziju- zemljopisnu duljinu, širinu i nadmorsku visinu kako bismo odredili položaj neke točke u ovom trodimenzionalnom svijetu. (Ovdje još uvijek govorimo o nasljeđu Euklidske geometrije).

  Fraktal planine Mandelbrot, proučavajući nepravilnosti prirode pritom zaklučuje kako te nepravilnosti često ispadaju vrlo pravilne. Za naziv, kojim bi obuhvatio svoje likove, dimenzije i geometriju kojom se služio, odabrao je latinski naziv fraktus za pridjev razlomljen ( od glagola frangere - razlomiti) te je stoga stvorio naziv fraktal.

"Fraktal je način promatranja beskraja."

"Zamislimo trokut sa svakom stranicom dugom 30cm, zatim zamislimo određenu transformaciju - dobro određen, lako ponovljivi skup pravila. Uzmimo srednju trećinu svake stranice i dodajmo na nju novi trokut, jednak oblikom, ali trećinom veličine. Rezultat je Davidova zvijezda. Umjesto tri stranice od trideset centimetara, ovaj lik sada ima dvanaest stranica od po deset cm. Umjesto tri, ima šest vrhova.
  Zatim, uzevši svaku od tih dvanaest stranica napravimo istu transformaciju. To možemo ponavljati u beskraj. Obris postaje sve razrađeniji. Podsjeća na neku vrstu idelane snježne pahuljice. Poznat je po imenu Kochine krivulje - gdje je krivulja svaka povezana ravna ili zaobljena crta... To je neprekinuta petlja koja se nikad ne presijeca jer su novi trokuti na svakoj stranici uvijek dovoljno maleni da izbjegnu moguće sudare. Svaka transformacija dodaje nešto površine unutarnjosti krivulje, ali ukupna površina ostaje konačna, u stvari ne mnogo veća od izvornog trokuta. Opišemo li oko izvornog trokuta kružnicu, Kochina krivulja je nikad neće prijeći."

  Nazivlje "Kochina pahuljica" potječe od imena Helge van Koch, švedske matematičarke koja ju je po prvi put opisala 1904. godine.

  Temeljem ovakvih svojstava Kochine krivulje, mnogi su zamislili i druge likove. Tako Sierpinskijev sag nastaje izrezivanjem jedne devetine kvadrata, nakon čega slijedi izrezivanje središta osam manjih kvadrata i tako dalje. Trodimenzijska analogija je Mengerova spužva, tijelo čvrstog izgleda beskonačno velike površine, ali obujma jednaka ništici.

  Korisnost Mandelbrotovih fraktala u razvrstavanju, opisivanju i mjerenju dijelova znanstvenog svijeta prepoznali su neki znanstvenioci poput Scholza, kojeg su veoma interesirale površine. Spoznaje fraktalne geometrije pomogle su znanstvenicima u proučavanju spajanja tvari, grananja i lomljenja. "To je način sagledavanja tvari: mikroskopski nazubljene površine metala, sitnih rupica i kanala porozne naftonosne stijene, razlomljenog krajolika trusnog područja."

  Prema Scholzu, opisivanje površine Zemlje vrlo je komplicirano u tom pogledu što se u gornjem čvrstom dijelu tla nalaze površine sa svojim pukotinama i rasjedima koji toliko dominiraju da su postali ključem svakog dobrog opisa. "Oni upravljaju tokom fluida kroz tlo - protokom nafte, vode i prirodnog plina. Upravljaju ponašanjem potresa." Geofizičari su na površine gledali kao na geometrijske likove. Pritom površina može biti ravna, ili imati određeni oblik. 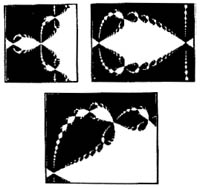Međutim, čak i ona površina koja ima izgled kakove krivulje, promatrana iz različitih kuteva i različitog gledišta otkriva sasvim nove informacije.
  Promatranje površine kroz euklidsku geometriju je kao "promatranje svemira kroz crveni filtar- vidjeli bismo određenu valnu duljinu svjetlosti, ali i propustili sve što se događa na valnim duljinama drugih boja..."(Stolz)
  Fraktalna geometrija omogućila je nove obzore prilikom promatranja površina Zemlje, kao i primjerice promatranja površine metala- fraktalne dimenzije mogu tako dati važne informacije o njegovoj čvrstoći.

  Pravila u nepravilnostima fraktalne geometrije našla su mjesta i u promatranju dodira površina: primjerice kod dodira automobilske gume s asfaltom. Činjenice govore da se površine u dodiru ne dodiruju posvuda. To sprečavaju neravnosti na površinama. Tako i u kamenu koji se nalazi pod velikim pritiskom ipak ostaje pukotine i omogućen je prohod fluida.

  Fraktalnu prirodu nalazimo i u primjeru krvih žila koje se granaju od aorti do kapilara - granaju se i granaju "dok ne postanu toliko uske da krvna zrnca moraju kroz njih klizati pojedinačno... Kao što Kochina krivulja ugura crtu beskonačne duljine u malu površinu, krvožilni sustav mora ugurati veliku površinu u ograničen obujam... Fraktalni ustroj prirode je izveo svoja djela tako uspješno da u većini stanica nikada nije više od tri ili četiri stanice udeljena od krvne žile."

  Fraktalni opisi ustroja ljudskog tijela dali su mnogima točniju sliku o stanju stvari. Počevši od promatranja bronhija, mokraćnog sustava, žući pa sve do srca "nekoliko kardiologa sklonih kaosu, ustanovilo je da frekvencijski spektar vremenskog usklađivanja kucanja srca, kao i potresi i pojave u gospodarstvu, slijedi fraktalne zakone i tvrdili su da jedan od ključeva za shvaćanje vremenskog usklađivanja kucanja srca je fraktalna organizacija His-Purkinjeove mreže, labirinta razgranatih putova organiziranih tako da su slične sebi u sve manjim i manjim mjerilima."

  Postavlja se pitanje kako je priroda uspjela složiti tako složeni ustroj. Ipak, prema Mandelbrotu fraktali, razgranati ustroji, opisuju se jednostavnošću, s vrlo malo informacija koje se vjerojatno nalaze i u samom DNK - "ako genske upute govore o broju i veličini bronhija, zar se ne bi moglo odrediti i ponovljeni postupak bifurkacije i razvoja."

  Govoreći o "sličnosti sebi" (selfsimilarity) govorimo o znanstvenom načelu koje je iščezlo pojavom fraktalne geometrije i razvojem tehnologije koja nam omogućuje pobliže promatranje. Naime, "sličnost sebi kao organizirajućeg načela proizašao je iz ograničenosti ljudskog iskustva s mjerilima. Kako drugačije zamisliti vrlo veliko i vrlo malo, vrlo brzo i vrlo sporo nego kao proširenje poznatoga. Mit je umro kad se ljudsko gledanje proširilo mikroskopom i teleskopom."

  "Pogledamo li primjer Newtonove metode primjenjene na traženje trećeg korijena od -1, vidimo podjelu ravnine na tri jednaka područja od kojih je jedan prikazan bijelom bojom. Sve bijele točke su privučene korijenu koji leži u najvećem bijelom području; sve crne točke privučene su jednom od preostala dva korijena. Granica ima neobično svojstvo da svaka točka na njoj graniči sa sva tri područja. I, kao što umeci pokazuju, povećani dijelovi otkrivaju fraktalni ustroj, ponavljajući temeljni uzorak na sve manjim mjerilima."

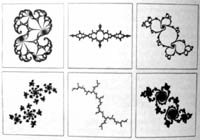
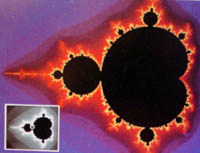
  Mnogi fraktalni oblici mogu se stvarati ponavljanim postupcima na kompleksnoj ravnini, ali samo je jedan Mandelbrotov skup. Počeo se pojavljivati kad je Mandelbrot pokušao pronaći način uopćavanja u svezi s razredom oblika poznatih kao Julijin skup- "neki Julijini skupovi su poput krugova pričvršćenih i deformiranih na mnogim mjestima kako bi im se dala fraktalna struktura. drugi su razbijeni na zasebna područja, a treći su nepovezane mrvice. Ali ni riječi ni koncepti euklidske geometrije ne mogu ih opisati."

  Francuski matematičar Douady je za Julijine skupove rekao: "neki su poput debelih oblaka, a drugi poput mršavog grma borovnica, neki izgledaju kao iskre koje plove zrakom nakon vatrometa: jedan ima oblik zeca, a mnogi imaju repove morskih konjica."

  Mandelbrotov skup je zbirka točaka. Svaka točka na kompleksnoj ravnini, tj. svaki kompleksni broj, ili je u skupu ili izvan njega. Jedan od načina određenja skupa jest ispitivanje svake točke. "Kako bismo ispitali točku, uzet ćemo kompleksni broj, kvadriramo ga, dodamo prvobitni broj, kvadriramo rezultat- i tako dalje. Ako zbroj ode u beskonačno, onda točka nije u Mandelbrotovom skupu. Ako broj ostane konačan, onda jest."

  Na pitanje povezanosti spominjane fraktalnosti i ritmu u prirodi o kojem govorimo odgovorit će vam sljedeći primjer:
  Što je oblik fraktalniji, jednostavnija su njemu odgovarajuća pravila. Za Kochinu pahuljicu i Sierpinskijevu brtvu trebalo je ukloniti dijelove crta i zamijeniti ih određenim likovima.
  Upotrijebivši umjesto toga igru kaosa, Michael Barnsey je izradio slike koje su započinjale kao zamagljene karikature i postajale sve jasnije. Nije bio potreban postupak ispravljanja: samo jedan skup pravila koji utjelovljuje konačni oblik.
  Barnsey i njegovi suradnici krenuli su u program stvaranja slika. Ključno pitanje je bilo kako uz određeni lik odabrati skup pravila. Odgovor koji je on nazvao "teoremom kolaža" bio je tako silno jednostavno opisati da su mnogi smatrali da je riječ o triku.
  Počinje se s crtanjem lika koji želimo reproducirati. Barnsey je za jedan od svojih prvih pokusa upotrijebio paprat. Zatim se koristeći računalni termin i miša za bilježenje točaka, preko izvornog lika dodaju njegove reducirane kopije koje se mogu i neuredno preklapati. Vrlo fraktalan lik može se lako oblikovati naslagama slojeva vlastitih kopija, manje frkatalan manje lako, ali svaki se lik može oblikovati slaganjem slojeva. Ako je slika složena, i pravila će biti složena. S druge strane, ako objekt ima fraktalni red u sebi, a znanstveno opažanje je da priroda često ima taj skriveni red, tad će ga biti moguće dekodirati sa svega nekoliko pravila. Model je tada zanimljiviji nego model izrađen prema euklidskoj geometriji jer znamo da kad gledamo rub lista biljke ne vidimo ravne crte.

  Barnsley je tvrdio da priroda igra vlastitu inačicu kaosa. U sporu iz koje izrasta paprat može se smjestiti ograničena količina informacija. Dakle, postoji ograničenje razrađenosti do koje može izrasti paprat.
  Nije čudno što možemo pronaći odgovarajuću sažetu informaciju kojom ćemo opisati tu paprat. Neki, s tim u skladu, smatraju da ćemo, jednog dana kada shvatimo kako je mozak organiziran, ostati začuđeni u postojanje sheme izgradnje mozga koja je zapravo vrlo jednostavna.

  Zaključili bismo dakle da geometrija koju i dan danas uzimamo kao polazišnu ne daje prave odgovore kada je riječ o prirodi, njezinim oblicima i ritmu.
  Čak i geometrijsku pravilnost koju su prepoznavali i arhitekti u svojim četvrtastim građevinama, zamijenili su novi pogledi. "Jednostavni oblici su nečovječni. Ne uspijevaju biti u skladu s načinom na koji se priroda sama organizira ili s načinom ljudskog viđenja svijeta."